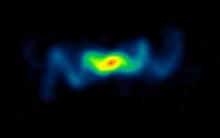
A computer simulation shows two black holes locked in a tight orbit around each other. The black holes are so close together that they will soon merge, emitting an enormous blast of gravitational waves. Detectors on Earth have discovered more than a dozen such mergers in the last few years. [The SXS Project]
You are here
Double Black Holes
The galaxy is full of binary star systems — two stars bound together by gravity. The list includes pairs of massive stars. And when those stars die, they can leave behind heavy but invisible corpses: black holes.
Astronomers haven’t seen a single black-hole binary. That’s not surprising, since black holes produce no energy. We know such binaries exist, though, because astronomers can hear them. They’ve detected the mergers of binary black holes as they spiral together.
A black-hole binary can form when the cores of two paired supergiant stars collapse. It also can form when two non-paired black holes stage a gravitational encounter with a third star. The third one gets kicked away, while the black holes become bound to each other.
Scientists have discovered the mergers of about a dozen black-hole binaries. They “listened” for gravitational waves — ripples in space-time created by the merging black holes.
The first merger was discovered four years ago. As the black holes got closer, they orbited faster, causing them to emit more waves.
Astronomers found that both black holes were at least 30 times the mass of the Sun. And in the last 20 milliseconds before they merged, they produced more energy — in the form of gravitational waves — than all the energy produced by all the visible stars in the universe. The waves carried away the equivalent of three times the mass of the Sun — waves that confirmed the existence of binary black holes.
Script by Damond Benningfield
Get Premium Audio
Listen to today's episode of StarDate on the web the same day it airs in high-quality streaming audio without any extra ads or announcements. Choose a $8 one-month pass, or listen every day for a year for just $30.